 |
|
|
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| หน้าหลัก | บทที่ 1 | บทที่ 2 | บทที่ 3 | บทที่ 4 | บทที่ 5 | บทที่ 6 | บทที่ 7 | บทที่ 8 | บทที่ 9 | บทที่ 10 | บทที่ 11 | บทที่ 12 | บทที่ 13 | บทที่ 14 | บทที่ 15 | |
บทที่ 11 การกลิ้ง ทอร์ค และโมเมนต์ตัมเชิงมุม
เมื่อวัตถุหมุน สามารถอธิบายได้ในเทอมของทอร์คและพลังงานจลน์ในการหมุน แต่ทอร์คสามรถเขียนอยู่ในรูปของเวกเตอร์ได้ เมื่อแรงมีผลต่อการเปลี่ยนแปลงโมเมนตัมเชิงเส้น ทอร์คก็ย่อมมีผลต่อการเปลี่ยนแปลงโมเมนตัมเชิงมุมด้วยเช่นกัน อาศัยความคล้ายกันโดยใช้กฎการอนุรักษ์โมเมนตัมเชิงเส้นเราจะได้กฎการอนุรักษ์โมเมนตัมเชิงมุม
11.1 ทอร์คในรูปของเวกเตอร์
11.2 โมเมนตัมเชิงมุมและทอร์ค
11.3 กฎการอนุรักษ์โมเมนตัมเชิงมุม
11.4 ไจโรสโคป
คำถาม เมื่อแตะฟุตบอลให้หมุน ทำไมฟุตบอลจึงไม่รักษาทิศทางการเคลื่อนที่
11.1 ทอร์คในรูปของเวกเตอร์
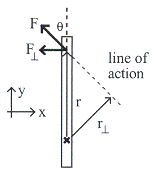 จากบทที่แล้ว
ขนาดของทอร์คคือผลคูณของแรงที่ลากไปตั้งฉาก
จากบทที่แล้ว
ขนาดของทอร์คคือผลคูณของแรงที่ลากไปตั้งฉาก ![]() กับแขนหมุน
กับแขนหมุน ![]() หรือผลคูณของแขนหมุนที่ลากไปตั้งฉาก
หรือผลคูณของแขนหมุนที่ลากไปตั้งฉาก
![]() กับแนวแรง
กับแนวแรง ![]() ดังรูปที่ 11.1
ดังรูปที่ 11.1
![]() =
= ![]() =
= ![]()
สมการที่ได้จะคล้ายกับผลคูรแบบครอส สามารถเขียนใหม่ได้เป็น
![]() =
= ![]()
รูปที่ 11.1
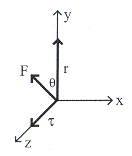 หมายความว่าตามรูปที่
11.1 ทิศของทอร์คจะมีทิศพุ่งออกจากระนาบของหน้ากระดาษ (ตามแกน
หมายความว่าตามรูปที่
11.1 ทิศของทอร์คจะมีทิศพุ่งออกจากระนาบของหน้ากระดาษ (ตามแกน ![]() ) ตามรูปที่ 11.2
เพื่อไม่ให้ยุ่งยากในการคิดจึงนำมากล่าวในบทนี้ เนื่องจากทิศของทอร์คจะขึ้นอยู่กับระนาบที่วัตถุหมุน
ในกรณีนี้เมื่อวัตถุหมุนในระนาบ
) ตามรูปที่ 11.2
เพื่อไม่ให้ยุ่งยากในการคิดจึงนำมากล่าวในบทนี้ เนื่องจากทิศของทอร์คจะขึ้นอยู่กับระนาบที่วัตถุหมุน
ในกรณีนี้เมื่อวัตถุหมุนในระนาบ ![]() ปัญหาที่น่าสนใจคือทอร์คเป็นเวกเตอร์และมีค่าคงที่
จะมีทิศเพียงทิศเดียวเท่านั้นที่ตั้งฉากกับระนาบ
ปัญหาที่น่าสนใจคือทอร์คเป็นเวกเตอร์และมีค่าคงที่
จะมีทิศเพียงทิศเดียวเท่านั้นที่ตั้งฉากกับระนาบ ![]() นั่นคือแกน
นั่นคือแกน ![]()
แต่เนื่องจากทิศที่ตั้งฉากกับระนาบ ![]() มีสองทิศคือ
มีสองทิศคือ ![]()
กับ ![]() เพื่อให้เป็นไปในทางเดียวกันเราใช้กฎมือขวาในการกำหนดทิศทาง
เพื่อให้เป็นไปในทางเดียวกันเราใช้กฎมือขวาในการกำหนดทิศทาง
รูปที่ 11.2
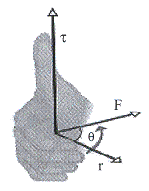
กฎมือขวา
- ให้นิ้วทั้งสี่ชี้ตามทิศของ
![]()
- กำนิ้วทั้งสี่เข้าหาแรง
![]()
- นิ้วหัวแม่มือจะแสดงทิศของทอร์ค
![]()
รูปที่ 1.3 กฎมือขวา
ตัวอย่างที่
11.1
ไม้เมตรมวล
![]() วางอยู่ในแนวราบปลายด้านหนึ่งชี้ไปทางทิศเหนือปลายอีกด้านหนึ่งตรึงติดอยู่กับที่
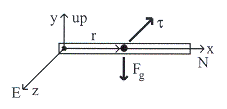
เมื่อปล่อยให้ไม้เมตรเคลื่อนที่ดังรูปที่ 11.4 จงหาทอร์คที่เกิดจากแรงโน้มถ่วง
วางอยู่ในแนวราบปลายด้านหนึ่งชี้ไปทางทิศเหนือปลายอีกด้านหนึ่งตรึงติดอยู่กับที่
เมื่อปล่อยให้ไม้เมตรเคลื่อนที่ดังรูปที่ 11.4 จงหาทอร์คที่เกิดจากแรงโน้มถ่วง
 วิธีทำ
จากนิยามของทอร์ค
วิธีทำ
จากนิยามของทอร์ค
![]() =
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
รูปที่ 11.4 จากกฎมือขวาทอร์คจะมีทิศตามทิศตะวันตก (แกน![]() )
)
11.2 โมเมนตัมเชิงมุมและทอร์ค
อาศัยกฎการเคลื่อนที่ข้อสองของนิวตันและนิยามของความเร่งจะได้นิยามของโมเมนตัมเชิงเส้น
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
![]() =
= ![]()
ในทำนองเดียวกันอาศัยกฎข้อสองของนิวตันสำหรับการหมุนและนิยามของความเร่งเชิงมุม จะได้สมการโมเมนตัมเชิงมุมของวัตถุแข็งเกร็ง
![]() =
= ![]()
= ![]()
= ![]()
= ![]()
![]() =
= ![]()
กฎข้อสองของนิวตันสำหรับการหมุน
![]() =
= ![]()
โมเมนตัมเชิงมุมของวัตถุแข็งเกร็ง
![]() =
= ![]()
ตัวอย่างที่
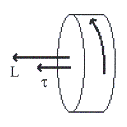
11.2 หินลับมีดมวล
![]() รัศมี
รัศมี ![]() ถูกเร่งให้มีความเร็ว
ถูกเร่งให้มีความเร็ว ![]() ในเวลา
ในเวลา
![]() จากเดิมอยู่นิ่งดังรูปที่ 11.5
จากเดิมอยู่นิ่งดังรูปที่ 11.5
 ก. จงหาค่าโมเมนตัมเชิงมุมสุดท้าย
ก. จงหาค่าโมเมนตัมเชิงมุมสุดท้าย
ข. ทอร์คสุทธิ์
วิธีทำ ก. โมเมนตัมเชิงมุมของวัตถุแข็งเกร็ง
![]() =
= ![]()
เมื่อแผ่นหินลับมีดคล้ายแผ่นจานจะได้โมเมนต์ความเฉื่อยคือ
![]() =
= ![]()
รูปที่ 11.5
= ![]()
= ![]()
ความเร็วเชิงมุมสุดท้ายคือ
![]() =
= ![]()
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
จากกฎข้อสองของนิวตันสำหรับการหมุน
![]() =
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
ความสัมพันธ์ระหว่างโมเมนตัมเชิงเส้นและโมเมนตัมเชิงมุม เป็นพื้นฐานสำหรับนิยามนิยามของโมเมนตัมเชิงมุม ความสัมพันธ์นี้มาจากการเปรียบเทียบนิยามของทอร์คและกฎข้อสองของนิวตันสำหรับการหมุน
![]() =
= ![]()
![]() =
= ![]()
= ![]()
เทอม ![]() เพิ่มเข้าไปในสมการค่าจะไม่เปลี่ยนแปลงเนื่องจากความเร็วครอสกับโมเมนตัมมีค่าเป็นศูนย์
จากนั้นอาศัยนิยามของความเร็วและผลของอนุพันธ์
เพิ่มเข้าไปในสมการค่าจะไม่เปลี่ยนแปลงเนื่องจากความเร็วครอสกับโมเมนตัมมีค่าเป็นศูนย์
จากนั้นอาศัยนิยามของความเร็วและผลของอนุพันธ์
![]() =
= ![]()
= ![]()
= ![]()
นิยามโมเมนตัมเชิงมุม
![]() =
= ![]()
ตัวอย่างที่ 11.3 จงหาโมเมนตัมเชิงมุมของดวงจันทร์เมื่อโคจรรอบโลกดังรูป
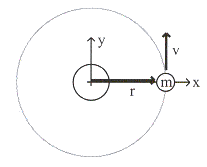 วิธีทำ
ข้อมูลสามารถค้นหาได้จากหนังสือฟิสิกส์ทั่ว ๆ ไป เมื่อ
วิธีทำ
ข้อมูลสามารถค้นหาได้จากหนังสือฟิสิกส์ทั่ว ๆ ไป เมื่อ ![]() ;
; ![]()
![]()
จากนิยามความเร็วและโมเมนตัม
![]() =
= ![]()
= ![]()
รูปที่ 11.6 =
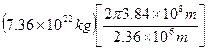 =
=
![]()
จากนิยามของโมเมนตัมเชิงมุม และอาศัยความจริงที่ว่ารัศมีโคจรกับความเร็วตั้งฉากกันจะได้
![]() =
= ![]()
![]() =
= ![]()
= ![]()
= ![]()
อาศัยกฎมือขวา โมเมนตัมเชิงมุมจะมีทิศพุ่งออกจากระนาบของกระดาษ
ตัวอย่างที่ 11.4 จงหาค่าโมเมนตัมเชิงมุมของวัตถุแข็งเกร็งโดยการประยุกต์ใช้นิยามของโมเมนตัมเชิงมุม
วิธีทำ จากรูปที่
11.7 พิจารณามวลก้อนเล็ก ๆ ![]() จากนั้นใช้นิยามของโมเมนตัมเชิงมุมและโมเมนตัมเชิงเส้น
จากนั้นใช้นิยามของโมเมนตัมเชิงมุมและโมเมนตัมเชิงเส้น
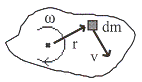
![]() =
= ![]()
![]() =
= ![]()
ให้จุดหมุนคงที่ รัศมีจะตั้งฉากกับความเร็ว โมเมนตัมเชิงมุมจะมีทิศพุ่งเข้าตั้งฉากกับระนาบของกระดาษทิศเดียวกับความเร็วเชิงมุม อาศัยความสัมพันธ์ระหว่างขนาดของความเร็วกับความเร็วเชิงมุม
รูปที่
11.7 ![]() =
= ![]() =
= ![]()
= ![]() =
= ![]()
เมื่อคิดทั้งก้อน
![]() =
= ![]()
![]() =
= 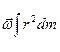
![]() =
= ![]()
11.3 กฎการอนุรักษ์โมเมนตัมเชิงมุม
จากกฎการอนุรักษ์โมเมนตัมเชิงเส้น และการประยุกต์ใช้กฎข้อสองสำหรับระบบอนุภาคเมื่อไม่มีแรงภายนอกมากระทำ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
กฎการอนุรักษ์โมเมนตัมเชิงเส้น “ในระบบโดดเดี่ยวผลรวมของโมเมนตัมเชิงเส้นจะมีค่าคงที่”
ในทำนองเดียวกันอาศัยกฎการอนุรักษ์โมเมนตัมเชิงมุมและการประยุกต์ใช้กฎข้อสองของการหมุนเมื่อไม่มีทอร์คภายนอกมากระทำ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
กฎการอนุรักษ์โมเมนตัมเชิงมุม “ในระบบโดเดี่ยวผลรวมของโมเมนตัมเชิงมุมจะคงที่” ตัวอย่างที่เห็นได้ชัดคือโต๊ะหมุนและกาแตะฟุตบอล
โต๊ะหมุน เมื่อยืนบนโต๊ะหมุนถ้ามีทอร์คภายนอกมากระทำโมเมนตัมเชิงมุมจะมีการเปลี่ยนแปลง
ฟุตบอล ถ้าไม่มีทอร์คกระทำบนลูกฟุตบอล ฟุตบอลจะเคลื่อนที่ในทิศทางเดียวกับโมเมนตัมเชิงมุม
โต๊ะหมุน เมื่อยืนบนโต๊ะหมุนถ้ามีการเปลี่ยนแปลงโมเมนความเฉื่อย ความเร็วเชิงมุมก็จะเปลี่ยนแปลงด้วยเพื่อให้โมเมนตัมเชิงมุมคงที่
ตัวอย่างที่
11.5
นักศึกษาคนหนึ่งยืนบนโต๊ะหมุนและกางแขนทั้งสองข้างออก
จากนั้นหดแขนเข้าแสดงดังรูปที่ 11.8 ทำให้ความเร็วเปลี่ยนจาก ![]() เป็น
เป็น ![]() จงหาอัตราส่วนโมเมนต์ความเฉื่อยที่เปลี่ยนไปต่อโมเมนต์ความเฉื่อยเดิม
จงหาอัตราส่วนโมเมนต์ความเฉื่อยที่เปลี่ยนไปต่อโมเมนต์ความเฉื่อยเดิม

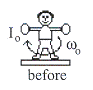 วิธีทำ
จากโมเมนตัมเชิงมุมของวัตถุแข็งเกร็ง สำหรับโมเมนตัมเชิงมุมก่อนการเปลี่ยนแปลง
วิธีทำ
จากโมเมนตัมเชิงมุมของวัตถุแข็งเกร็ง สำหรับโมเมนตัมเชิงมุมก่อนการเปลี่ยนแปลง
![]() =
= ![]()
โมเมนตัมเชิงมุมภายหลังการเปลี่ยนแปลง
![]() =
= ![]()
รูปที่ 11.8
เมื่อไม่มีทอร์คภายนอกมากระทำจากกฎการอนุรักษ์โมเมนตัมเชิงมุม
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
= ![]()
จากคำตอบที่ได้แสดงว่าเมื่อความเร็วเชิงมุมเพิ่ม โมเมนต์ความเฉื่อยจะลดลงเพื่อให้โมเมนตัมเชิงมุมคงที่ตามกฎการอนุรักษ์พลังงาน
ตัวอย่างที่
11.6
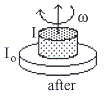
แป้นหมุนของช่างปั้นหม้อมีโมเมนต์ความเฉื่อย ![]() หมุนด้วยความเร็ว
หมุนด้วยความเร็ว ![]() ถ้ามีดินเหนียวรูปทรงกระบอกมวล
ถ้ามีดินเหนียวรูปทรงกระบอกมวล
![]() รัศมี
รัศมี ![]() เคลื่อนลงมาตามแนวดิ่งและตกลงตรงจุดศูนย์กลางของแป้นหมุนดังรูปที่
11.9 จงหาอัตราการหมุนเมื่อก้อนดินเหนียวตกลงบนแป้นหมุน
เคลื่อนลงมาตามแนวดิ่งและตกลงตรงจุดศูนย์กลางของแป้นหมุนดังรูปที่
11.9 จงหาอัตราการหมุนเมื่อก้อนดินเหนียวตกลงบนแป้นหมุน
วิธีทำ จากโมเมนตัมเชิงมุมของวัตถุแข็งเกร็งจะได
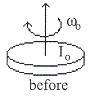 โมเมนตัมเชิงมุมเริ่มต้น (มีเฉพาะแป้นหมุน)
โมเมนตัมเชิงมุมเริ่มต้น (มีเฉพาะแป้นหมุน)
![]() =
= ![]()
โมเมนตัมเชิงมุมสุดท้าย (ประกอบด้วยแป้น หมุนและดินน้ำมัน)
รูปที่ 11.9
![]() =
= ![]()
แต่ดินน้ำเหนียวเป็นรูปทรงกระบอกมีโมเมนต์ความเฉื่อยเป็น
![]()
![]() =
= ![]()
เมื่อไม่มีทอร์คภายนอกมากระทำ จะได้ว่าโมเมนตัมเชิงมุมไม่มีการเปลี่ยนแปลง อาศัยการอนุรักษ์โมเมนตัมเชิงมุม
![]() =
= ![]()
![]() =
= 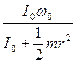
= 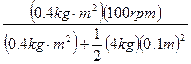
= ![]()
11.4 ไจโรสโคป
ไจโรสโคป ประกอบด้วยล้อหมุนซึ่งติดตั้งไว้บนแกนในลักษณะซึ่งแกนจะหมุนเปลี่ยนทิศทางได้อย่างอิสระดังรูปที่ 11.10
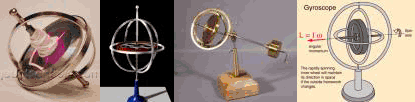
รูปที่ 11.10
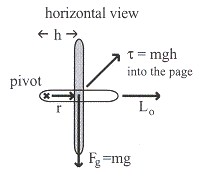 เมื่อไจโรสโคปหมุนจะเกิดทอร์คเนื่องจากน้ำหนักของไจโรสโคป
ซึ่งขนาดและทิศทางของทอร์คหาได้จากสมการ
เมื่อไจโรสโคปหมุนจะเกิดทอร์คเนื่องจากน้ำหนักของไจโรสโคป
ซึ่งขนาดและทิศทางของทอร์คหาได้จากสมการ
![]() =
= ![]()
พิจารณารูปที่ 11.11 เมื่อมองจากด้านข้าง
![]() =
= ![]()
= ![]()
(เพราะว่า
![]() )
)
จากกฎมือขวาทอร์คมีทิศพุ่งเข้าระนาบของกระดาษเนื่องจากทอร์ค
![]() ตั้งฉากกับโมเมนตัมเชิงมุม
ตั้งฉากกับโมเมนตัมเชิงมุม
![]() ทำให้การพิจารณาการหมุนมีความยุ่งยาก
ให้คิด
ทำให้การพิจารณาการหมุนมีความยุ่งยาก
ให้คิด
รูปที่ 11.11 เปรียบเทียบความคล้ายกันระหว่างแรงที่กระทำตั้งฉากกับโมเมนตัมเชิงเส้น ซึ่งจะทำให้เกิดการหมุนเป็นวงกลม ซึ่งเราคาดว่าคงจะมีผลเช่นเดียวกันกับเมื่อทอร์คกระทำตั้งฉากกับโมเมนตัมเชิงมุม
ทอร์คลัพธ์จะเกิดจาการเปลี่ยนแปลงโมเมนตัมเชิงมุม
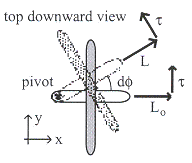
ถ้าให้ทอร์คมีทิศตั้งฉากกับโมเมนตัมเชิงมุมเริ่มต้น ![]() ขนาดของโมเมนตัมเชิงมุมจะไม่เปลี่ยนแปลงเฉพาะทิศทางเท่านั้นดังรูปที่
11.12 เมื่อมองจากด้านบนลงมาจะสังเกตเห็นว่ามุมเปลี่ยนไป
ขนาดของโมเมนตัมเชิงมุมจะไม่เปลี่ยนแปลงเฉพาะทิศทางเท่านั้นดังรูปที่
11.12 เมื่อมองจากด้านบนลงมาจะสังเกตเห็นว่ามุมเปลี่ยนไป ![]() เมื่อหาค่าโมเมนความเฉื่อยของไจโรสโคป
อาศัยกฎข้อสองของการหมุน
เมื่อหาค่าโมเมนความเฉื่อยของไจโรสโคป
อาศัยกฎข้อสองของการหมุน
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
รูปที่ 11.12
เมื่อพิจารณาโดยใช้เวกเตอร์ซึ่งแสดงดังรูปที่ 11.13
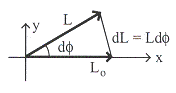
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
รูปที่ 11.13
แต่ไจโรสโคปคือวัตถุแข็งเกร็งที่หมุนรอบแกนที่หมุนรอบแกนของความเร็วเชิงมุม ดังนั้นขนาดโมเมนตัมเชิงมุมของไจโรสโคปคือ
![]() =
= ![]()
![]() =
= ![]()
![]() =
= ![]()
การเคลื่อนที่ของแกนรอบแนวดิ่งนี้เรียกว่า การหมุนควง (precession)
แทนด้วยอักษรกรีก ![]() จะได้
จะได้
![]() =
= ![]()
สรุป
กฎข้อสองของนิวตันสำหรับการหมุน : ![]()
โมเมนตัมเชิงมุมของวัตถุแข็งเกร็ง : ![]()
นิยามของโมเมนตัมเชิงมุม
: ![]()
กฎการอนุรักษ์โมเมนตัมเชิงมุม
: ![]()